Με Ταρούν
Λοιπόν τα κλάσματα μπορεί να είναι πραγματικά τρομακτικά, πρέπει να ομολογήσω. Η προσθήκη κλασμάτων είναι ακόμη πιο τρομακτική. Φαίνεται ότι είναι το σημείο εκκίνησης της λιτότητας του κόσμου των μαθηματικών. Μέχρι να συνειδητοποιήσετε ότι η αντιμετώπιση των κλασμάτων είναι επίσης τόσο απλή όσο η αντιμετώπιση των φυσικών αριθμών, αν γνωρίζετε το τέχνασμα.
Μέθοδοι προσθήκης κλασμάτων
Μέθοδος 1
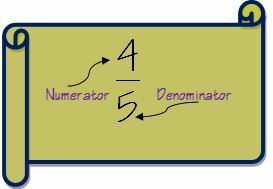
1. Πρώτα ας κατανοήσουμε την ορολογία των κλασμάτων πριν προχωρήσουμε σε βήματα για την προσθήκη κλασμάτων. Ένα κλάσμα έχει δύο μέρη: αριθμητή και παρονομαστή. Εάν θέλετε πραγματικά να γίνετε μελετητής στο Fractions μπορείτε να επισκεφτείτε το Κλασματική σελίδα στη Wikipedia.
Ο αριθμητής είναι ο αριθμός πάνω από τη γραμμή σε κλάσμα και ο παρονομαστής είναι ο αριθμός κάτω από τη γραμμή.
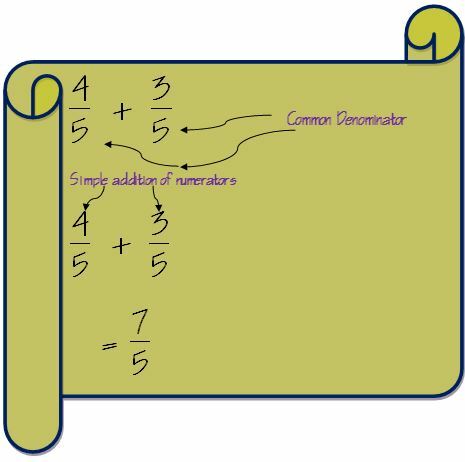
Το πρώτο βήμα για την προσθήκη κλασμάτων είναι να ελέγξετε τους παρονομαστές των δύο κλασμάτων. Ο παρονομαστής και για τα δύο κλάσματα είναι ίδιος, τότε η προσθήκη γίνεται πολύ απλή.
Σε μια τέτοια περίπτωση απλώς πρέπει να προσθέσουμε τους αριθμητές και ο παρονομαστής θα παραμείνει ο ίδιος.
Αλλά αν οι παρονομαστές δεν είναι ίδιοι, τότε πρέπει να κάνουμε τους παρονομαστές και των δύο κλασμάτων ίδιο. Η μέθοδος που πρέπει να κάνετε είναι να βρείτε το λιγότερο κοινό πολλαπλάσιο των παρονομαστών.
Πώς να βρείτε το λιγότερο κοινό πολλαπλό
Ας πούμε ότι πρέπει να βρούμε LCM δύο αριθμών 8 και 12.
Καταγράψτε πρώτα τους πρωταρχικούς παράγοντες των δύο αριθμών ξεχωριστά.
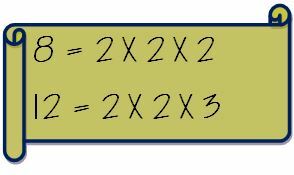
Τώρα βγάλτε τους κοινούς παράγοντες και πολλαπλασιάστε τον με τους μη κοινούς παράγοντες. Έτσι, το LCM των 8 και 12 θα υπολογιστεί ως εξής.
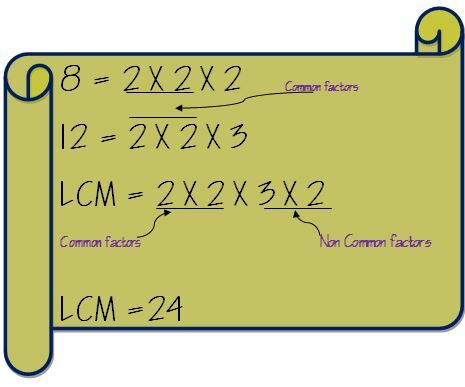
Προσθέστε κλάσματα με διαφορετικούς παρονομαστές
Ας πούμε ότι έχουμε δύο κλάσματα 3/8 και 5/12
Τα βήματα είναι:
1. Ελέγξτε εάν οι παρονομαστές είναι ίδιοι και για τα δύο κλάσματα. Εάν οι παρονομαστές είναι ίδιοι, ακολουθούμε τη μέθοδο που αναφέρεται παραπάνω. Στην περίπτωσή μας είναι διαφορετικά.
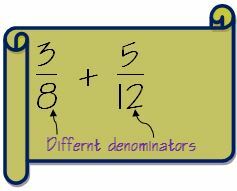
2. Μάθετε το LCM του παρονομαστή. Όπως απεικονίζεται παραπάνω, το LCM για 8 και 12 είναι 24.
3. Κάντε και τους δύο παρονομαστές ίδιο με το LCM πολλαπλασιάζοντας με κατάλληλους αριθμούς.
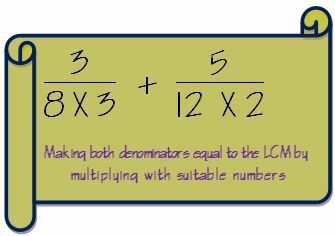
4. Αν έχουμε πολλαπλασιάσει τον παρονομαστή με έναν αριθμό, τότε πρέπει επίσης να πολλαπλασιάσουμε τον αριθμητή με τον ίδιο αριθμό, για να διατηρήσουμε το κλάσμα ανέπαφο.

5. Με την εκτέλεση αυτών των βημάτων έχουμε δύο κλάσματα των οποίων οι παρονομαστές είναι ίδιοι. Απλώς πρέπει να προσθέσουμε τους αριθμητές όπως κάναμε στο προηγούμενο παράδειγμα.

6. Έχουμε το αποτέλεσμα στις 19/24
7. Πρέπει να ελέγξουμε εάν υπάρχει κοινός παράγοντας μεταξύ του αριθμητή και του παρονομαστή ή όχι μετά την πραγματοποίηση της προσθήκης.
8. Εάν δεν υπάρχει κοινός παράγοντας, τότε μπορούμε να αναφέρουμε το αποτέλεσμα ως την τελική μας απάντηση.

Μέθοδος 2
Αυτή η μέθοδος θα μας δώσει επίσης το επιθυμητό αποτέλεσμα, αλλά δεν προτείνεται για μαθητές πέμπτης τάξης που θέλουν να μάθουν να προσθέτουν κλάσματα.
1. Μετατρέψτε και το κλάσμα σε αριθμούς διαιρώντας τον αριθμητή με τον παρονομαστή

2. Τώρα είναι απλή προσθήκη δύο αριθμών
3. Προσθέστε τους δύο αριθμούς για να λάβετε την απάντηση

Λάβετε υπόψη ότι οι απαντήσεις που λάβαμε στη Μέθοδο 1 και τη Μέθοδο 2 για την προσθήκη κλασμάτων είναι ίδιες. Η απάντηση με τη μέθοδο 1 είναι 19/24. Εάν διαιρέσουμε το 19 με το 24, θα λάβουμε την απάντηση ως 0,779, δηλαδή αυτό που έχουμε με τη μέθοδο 2.