Од стране Тарун
Па, разломци могу бити заиста застрашујући, морам признати. Додавање разломка је чак страшније. Чини се да су они полазна тачка застрашујућег света математике. Док не схватите да је бављење разломцима такође једноставно као и бављење природним бројевима, ако знате трик.
Методе за додавање разломака
Метод 1
1. Прво да схватимо терминологију разломака пре него што пређемо на кораке за додавање разломака. Разломак има два дела - бројилац и називник. Ако заиста желите да постанете научник у разломку, можете посетити Страница разломка на Википедији.
Нумератор је број изнад линије у разломку, а називник је број испод линије.
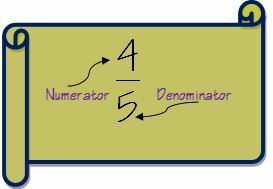
Први корак за додавање разломака је провера називника два разломка. Ако је називник за обе разломке исти, онда сабирање постаје врло једноставно.
У таквом случају морамо само додати бројалице и називник ће остати исти.
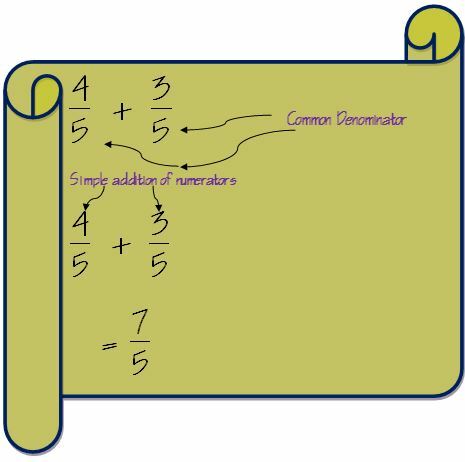
Али ако именитељи нису исти, тада морамо направити именитеље обе фракције једнаким. Метода коју треба урадити је проналажење најмањег заједничког вишекратника називника.
Како пронаћи најмање заједнички вишекратник
Рецимо да морамо пронаћи ЛЦМ два броја 8 и 12.
Прво запишите просте чиниоце два броја одвојено.
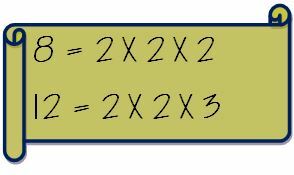
Сада извадите заједничке факторе и помножите их са необичним факторима. Дакле, ЛЦМ од 8 и 12 израчунаваће се на следећи начин.
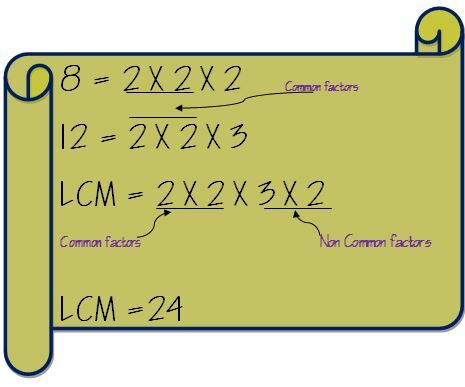
Додајте разломке са различитим имениоцима
Рецимо да имамо две фракције 3/8 и 5/12
Кораци су:
1. Проверите да ли су именитељи исти за оба разломка. Ако су називници исти, следимо горе поменуту методу. У нашем случају су различити.
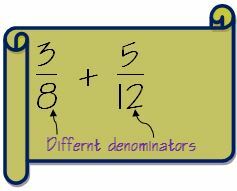
2. Сазнајте ЛЦМ називника. Као што је илустровано изнад, ЛЦМ за 8 и 12 је 24.
3. Нека оба именитеља буду иста као ЛЦМ множењем са одговарајућим бројевима.
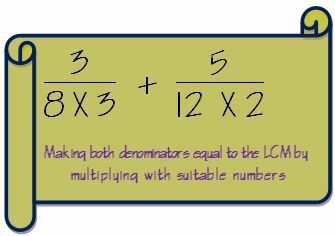
4. Ако смо помножили називник са бројем, такође морамо помножити и бројилац са истим бројем да бисмо разломак сачували нетакнутим.

5. Извођењем ових корака добијамо два разломка чији су називници исти. Дакле, морамо само додати бројилице као што смо то чинили у нашем ранијем примеру.

6. Резултат добијамо 19/24
7. Морамо да проверимо да ли постоји неки заједнички фактор између бројила и називника или не након што се изврши сабирање.
8. Ако не постоји заједнички фактор, резултат можемо пријавити као коначни одговор.

Метод 2
Ова метода ће нам такође дати жељени резултат, али није препоручена за ученике петог разреда који желе да науче да додају разломке.
1. Претворите оба разломка у бројеве тако што ћете поделити бројилац са називником

2. Сада је то једноставно сабирање два броја
3. Додајте два броја да бисте добили одговор

Имајте на уму да су одговори које смо добили у Методу 1 и Методи 2 за додавање разломака исти. Одговор методом 1 је 19/24. Ако 19 поделимо са 24, добићемо одговор као 0,791, што смо добили методом 2.