От Тарун
Я должен признать, что дроби могут быть действительно страшными. Сложить дроби еще страшнее. Похоже, они являются отправной точкой пугающего мира математики. Пока вы не поймете, что работать с дробями так же просто, как с натуральными числами, если вы знаете этот трюк.
Способы добавления дробей
Способ 1
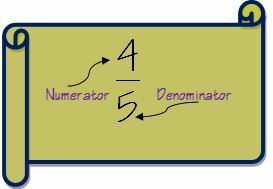
1. Сначала давайте разберемся с терминологией дробей, прежде чем переходить к шагам по сложению дробей. Дробь состоит из двух частей - числителя и знаменателя. Если вы действительно хотите стать ученым по фракциям, вы можете посетить Страница фракций в Википедии.
В числителе указывается число над чертой в виде дроби, а в знаменателе - число под чертой.
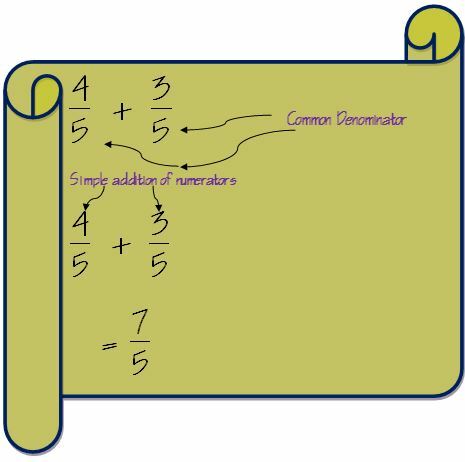
Первый шаг к сложению дробей - это проверка знаменателей двух дробей. Если знаменатели обеих дробей одинаковы, сложение становится очень простым.
В таком случае нам просто нужно сложить числители, и знаменатель останется прежним.
Но если знаменатели не совпадают, тогда нам нужно сделать знаменатели обеих дробей одинаковыми. Метод состоит в том, чтобы найти наименьшее общее кратное знаменателей.
Как найти наименьшее общее кратное
Допустим, нам нужно найти НОК двух чисел 8 и 12.
Сначала запишите по отдельности простые множители двух чисел.
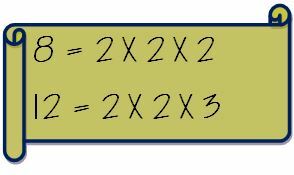
Теперь выньте общие множители и умножьте их на необщие множители. Таким образом, НОК 8 и 12 будет рассчитываться следующим образом.
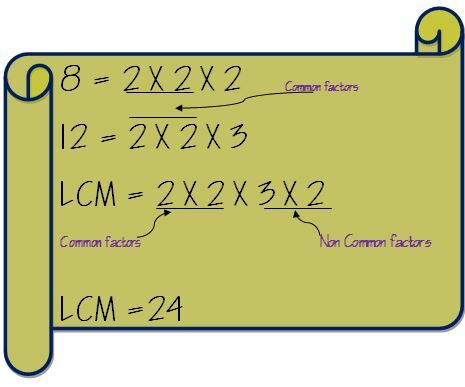
Сложите дроби с разными знаменателями
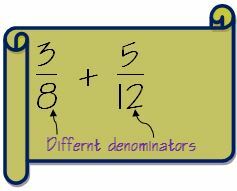
Скажем, у нас есть две дроби 3/8 и 5/12
Шаги следующие:
1. Проверьте, совпадают ли знаменатели для обеих дробей. Если знаменатели совпадают, мы следуем вышеупомянутому методу. В нашем случае они разные.
2. Найдите НОК знаменателя. Как показано выше, НОК для 8 и 12 равно 24.
3. Сделайте оба знаменателя такими же, как НОК, умножив на подходящие числа.
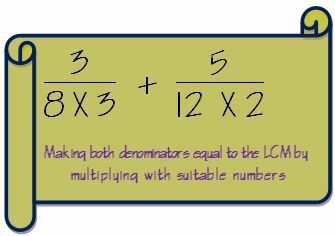
4. Если мы умножили знаменатель на число, нам также нужно умножить числитель на то же число, чтобы сохранить дробь нетронутой.

5. Выполнив эти действия, мы получим две дроби, знаменатели которых совпадают. Поэтому нам просто нужно добавить числители, как в нашем предыдущем примере.

6. Получаем результат как 19/24
7. Мы должны проверить, есть ли общий множитель между числителем и знаменателем после выполнения сложения.
8. Если нет общего фактора, мы можем сообщить результат в качестве окончательного ответа.

Способ 2
Этот метод также даст нам желаемый результат, но он не рекомендуется ученикам пятого класса, которые хотят научиться складывать дроби.
1. Преобразуйте обе дроби в числа, разделив числитель на знаменатель.

2. Теперь это простое сложение двух чисел.
3. Сложите два числа, чтобы получить ответ

Обратите внимание, что ответы, которые мы получили в методах 1 и 2 для сложения дробей, одинаковы. Ответ по методу 1 - 19/24. Если разделить 19 на 24, мы получим 0,791, что и было получено методом 2.