Przez Tarun
Cóż, ułamki mogą być naprawdę przerażające, muszę przyznać. Dodawanie ułamków jest jeszcze bardziej przerażające. Wygląda na to, że są punktem wyjścia do przerażającego świata matematyki. Dopóki nie zdasz sobie sprawy, że radzenie sobie z ułamkami jest również tak proste, jak radzenie sobie z liczbami naturalnymi, jeśli znasz tę sztuczkę.
Metody dodawania frakcji
Metoda 1
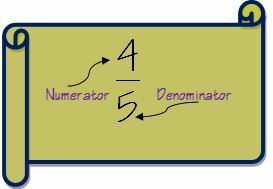
1. Najpierw zrozummy terminologię ułamków, zanim przejdziemy do kroków dodawania ułamków. Ułamek ma dwie części – licznik i mianownik. Jeśli naprawdę chcesz zostać naukowcem we frakcjach, możesz odwiedzić Strona frakcji w Wikipedii.
Licznik to liczba powyżej wiersza w ułamku, a mianownik to liczba poniżej wiersza.
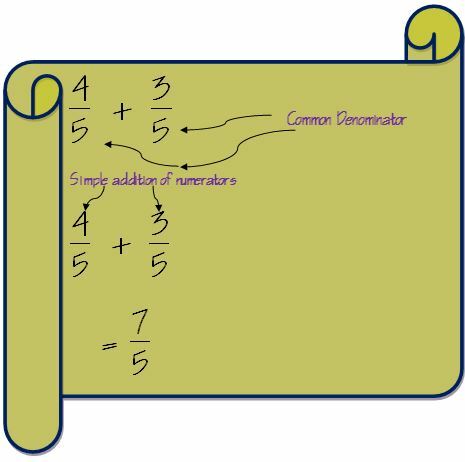
Pierwszym krokiem do dodania ułamków jest sprawdzenie mianowników dwóch ułamków. Jeśli mianownik dla obu frakcji jest taki sam, dodawanie staje się bardzo proste.
W takim przypadku wystarczy dodać liczniki, a mianownik pozostanie taki sam.
Ale jeśli mianowniki nie są takie same, musimy sprawić, by mianowniki obu ułamków były takie same. Metoda polega na znalezieniu najmniejszej wspólnej wielokrotności mianowników.
Jak znaleźć najmniejszą wspólną wielokrotność
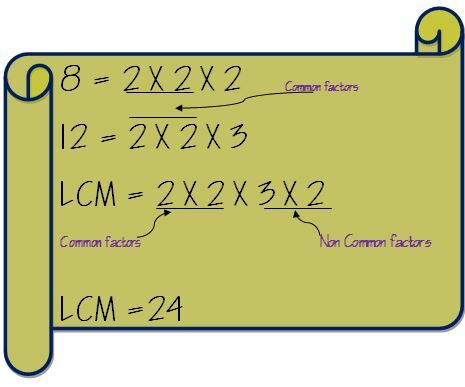
Powiedzmy, że musimy znaleźć LCM dwóch liczb 8 i 12.
Najpierw zapisz osobno czynniki pierwsze tych dwóch liczb.
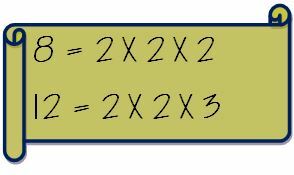
Teraz wyjmij wspólne czynniki i pomnóż je przez niewspólne czynniki. Tak więc LCM 8 i 12 zostanie obliczony w następujący sposób.
Dodaj ułamki o różnych mianownikach
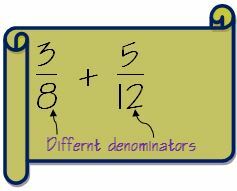
Powiedzmy, że mamy dwie ułamki 3/8 i 5/12
Kroki to:
1. Sprawdź, czy mianowniki są takie same dla obu ułamków. Jeśli mianowniki są takie same, stosujemy metodę opisaną powyżej. W naszym przypadku są różne.
2. Dowiedz się LCM mianownika. Jak pokazano powyżej, LCM dla 8 i 12 wynosi 24.
3. Uczyń oba mianowniki takimi samymi jak LCM, mnożąc przez odpowiednie liczby.
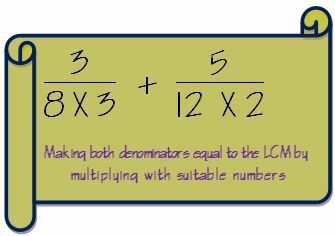
4. Jeśli pomnożyliśmy mianownik przez liczbę, musimy również pomnożyć licznik przez tę samą liczbę, aby zachować ułamek nienaruszony.

5. Wykonując te kroki otrzymujemy dwa ułamki, których mianowniki są takie same. Więc musimy tylko dodać liczniki, tak jak to zrobiliśmy w naszym poprzednim przykładzie.

6. Otrzymujemy wynik 19/24
7. Musimy sprawdzić, czy istnieje jakiś wspólny czynnik między licznikiem i mianownikiem, czy nie po wykonaniu dodawania.
8. Jeśli nie ma wspólnego czynnika, możemy zgłosić wynik jako naszą ostateczną odpowiedź.

Metoda 2
Ta metoda również da nam pożądany rezultat, ale nie jest zalecana dla uczniów piątej klasy, którzy chcą nauczyć się dodawać ułamki.
1. Zamień ułamek na liczby, dzieląc licznik przez mianownik

2. Teraz jest to proste dodanie dwóch liczb
3. Dodaj dwie liczby, aby uzyskać odpowiedź

Pamiętaj, że odpowiedzi, które otrzymaliśmy w Metodzie 1 i Metodzie 2, aby dodać ułamki, są takie same. Odpowiedź według metody 1 to 19/24. Jeśli podzielimy 19 przez 24, otrzymamy odpowiedź 0,791, co otrzymaliśmy metodą 2.