Foreslå en enklere måte å legge til brøker på

Brøkdeler kan være veldig skummelt, må jeg innrømme. Å legge til brøker er skumlere selv. Det virker som de er utgangspunktet for matematikkens skumhet. Inntil du innser at håndtering av brøker også er så enkelt som å håndtere naturlige tall, hvis du kjenner trikset.

Metoder for å legge til brøker

Metode 1

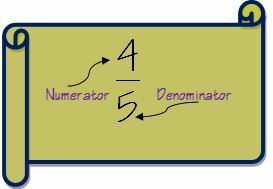
1. La oss først forstå terminologien til brøker før vi går til trinn for å legge til brøker. En brøkdel har to deler - teller og nevner. Hvis du virkelig vil bli en lærd i Fraksjoner, kan du besøke Brøkside på Wikipedia.

Teller er tallet over linjen i en brøkdel og nevneren er tallet under linjen.

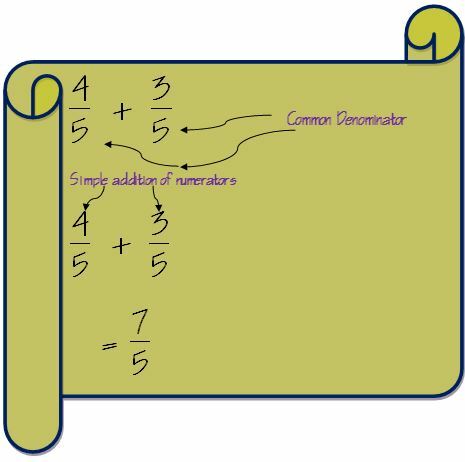
Det første trinnet for å legge til brøker er å kontrollere nevnere for de to brøkene. Det nevneren for begge brøkene er den samme, så blir tilsetning veldig enkel.

I et slikt tilfelle må vi bare legge til tellerne, og nevneren forblir den samme.

Men hvis nevnerne ikke er de samme, må vi gjøre nevnerne til begge brøkene like. Metoden å gjøre er å finne det minst vanlige multiple av nevnerne.

Hvordan finne minst vanlige multiple

Si at vi må finne LCM med to tall 8 og 12.

Skriv først hovedfaktorene til de to tallene hver for seg.

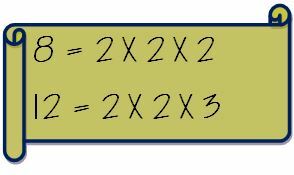
Ta nå ut de vanlige faktorene og multipliser den med de ikke-vanlige faktorene. Så LCM på 8 og 12 vil bli beregnet som følger.

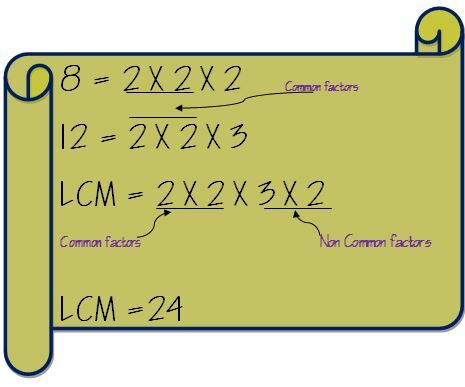
Legg til brøker med forskjellige nevnere

Si at vi har to brøker 3/8 og 5/12

Trinnene er:

1. Sjekk om nevnerne er like for begge brøkene. Hvis nevnerne er like, følger vi metoden nevnt ovenfor. I vårt tilfelle er de forskjellige.

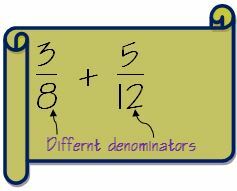
2. Finn ut LCM for nevneren. Som illustrert ovenfor er LCM for 8 og 12 24.

3. Gjør begge nevnerne like med LCM ved å multiplisere med passende tall.

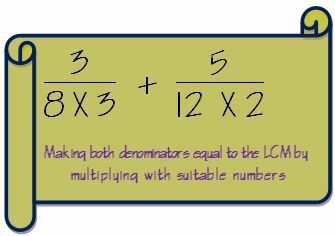
4. Hvis vi har multiplisert nevneren med et tall, må vi også multiplisere telleren med det samme tallet også for å holde brøken intakt.

5. Ved å utføre disse trinnene får vi to brøker der nevnere er like. Så vi må bare legge til tellerne som vi gjorde i vårt tidligere eksempel.

6. Vi får resultatet som 19/24

7. Vi må sjekke om det er noen felles faktor mellom teller og nevner eller ikke etter at tillegg er utført.

8. Hvis det ikke er noen felles faktor, kan vi rapportere resultatet som vårt endelige svar.

 Metode 2

Denne metoden vil også gi oss det ønskede resultatet, men det anbefales ikke for studenter i femte klasse som ønsker å lære å legge til brøker.

1. Konverter begge brøkdelene i tall ved å dele teller etter nevner

2. Nå er det enkelt å legge til to tall

3. Legg til de to tallene for å få svaret

Vær oppmerksom på at svarene vi fikk i metode 1 og metode 2 for å legge til brøker, er de samme. Svaret ved metode 1 er 19/24. Hvis vi deler 19 med 24, får vi svaret som 0,791, som er hva vi fikk ved metode 2.