Door Tarun
Nou, breuken kunnen heel eng zijn, moet ik toegeven. Het toevoegen van breuken is zelfs enger. Het lijkt alsof ze het startpunt zijn van de angst van de wereld van de wiskunde. Tot je je realiseert dat het omgaan met breuken ook net zo eenvoudig is als het omgaan met natuurlijke getallen, als je de truc kent.
Methoden om breuken toe te voegen
Methode 1
1. Laten we eerst de terminologie van breuken begrijpen voordat we naar de stappen gaan om breuken toe te voegen. Een breuk heeft twee delen: teller en noemer. Als je echt een geleerde in breuken wilt worden, kun je een bezoek brengen aan de Breukpagina op Wikipedia.
Teller is het getal boven de lijn in een breuk en de noemer is het getal onder de lijn.
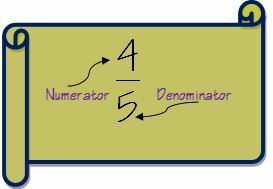
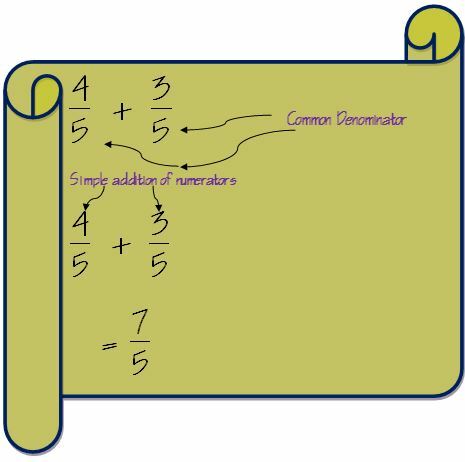
De eerste stap om breuken op te tellen is om de noemers van de twee breuken te controleren. Als de noemer voor beide breuken hetzelfde is, wordt optellen heel eenvoudig.
In zo'n geval hoeven we alleen de tellers op te tellen en de noemer blijft hetzelfde.
Maar als de noemers niet hetzelfde zijn, moeten we de noemers van beide breuken hetzelfde maken. De methode om dit te doen is om het kleinste gemene veelvoud van de noemers te vinden.
Hoe het kleinste gemene veelvoud te vinden?
Stel dat we LCM van twee getallen 8 en 12 moeten vinden.
Schrijf eerst de priemfactoren van de twee getallen apart op.
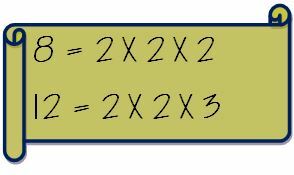
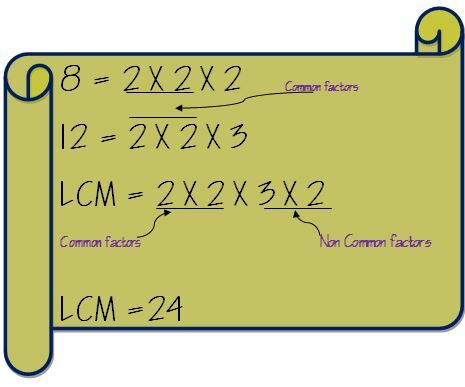
Haal nu de gemeenschappelijke factoren eruit en vermenigvuldig deze met de niet-gemeenschappelijke factoren. Dus de LCM van 8 en 12 wordt als volgt berekend.
Breuken met verschillende noemers optellen
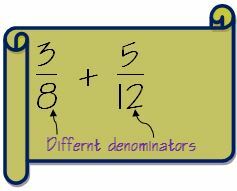
Stel dat we twee breuken 3/8 en 5/12. hebben
De stappen zijn:
1. Controleer of de noemers hetzelfde zijn voor beide breuken. Als de noemers hetzelfde zijn, volgen we de hierboven genoemde methode. In ons geval zijn ze anders.
2. Ontdek de LCM van de noemer. Zoals hierboven geïllustreerd is de LCM voor 8 en 12 24.
3. Maak beide noemers hetzelfde als de LCM door te vermenigvuldigen met geschikte getallen.
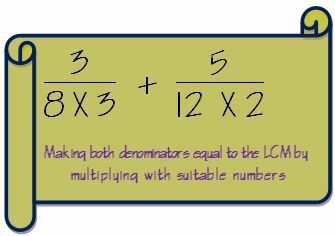
4. Als we de noemer met een getal hebben vermenigvuldigd, moeten we ook de teller met hetzelfde getal vermenigvuldigen om de breuk intact te houden.

5. Door deze stappen uit te voeren krijgen we twee breuken waarvan de noemers hetzelfde zijn. We hoeven dus alleen de tellers op te tellen zoals we deden in ons eerdere voorbeeld.

6. We krijgen het resultaat als 19/24
7. We moeten controleren of er een gemeenschappelijke factor is tussen de teller en de noemer of niet nadat de optelling is uitgevoerd.
8. Als er geen gemeenschappelijke factor is, kunnen we het resultaat rapporteren als ons definitieve antwoord.

Methode 2
Deze methode geeft ons ook het gewenste resultaat, maar wordt niet aanbevolen voor leerlingen van het vijfde leerjaar die willen leren breuken op te tellen.
1. Zet beide breuken om in getallen door de teller te delen door de noemer

2. Nu is het eenvoudig optellen van twee getallen
3. Voeg de twee cijfers toe om het antwoord te krijgen

Houd er rekening mee dat de antwoorden die we hebben gekregen in methode 1 en methode 2 om breuken op te tellen hetzelfde zijn. Het antwoord van methode 1 is 19/24. Als we 19 door 24 delen, krijgen we het antwoord als 0,791, wat we met methode 2 hebben gekregen.