Autors Tarun
Nu jāatzīst, ka labi frakcijas var būt patiešām biedējošas. Frakciju pievienošana ir briesmīgāka pat. Šķiet, ka tie ir matemātikas pasaules baisuma sākumpunkts. Līdz brīdim, kad jūs saprotat, ka nodarbošanās ar frakcijām ir tikpat vienkārša kā dabisko skaitļu apstrāde, ja jūs zināt triku.
Frakciju pievienošanas metodes
1. metode
1. Vispirms ļaujiet mums saprast frakciju terminoloģiju, pirms pāriet uz frakciju pievienošanas soļiem. Daļai ir divas daļas - skaitītājs un saucējs. Ja jūs patiešām vēlaties kļūt par zinātnieku frakcijās, varat apmeklēt Frakciju lapa Vikipēdijā.
Skaitītājs ir skaitlis virs līnijas frakcijā, un saucējs ir skaitlis zem līnijas.
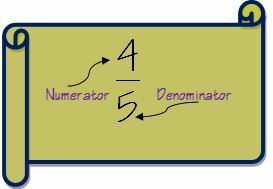
Pirmais solis frakciju pievienošanai ir pārbaudīt abu frakciju saucējus. Tas saucējs abām frakcijām ir vienāds, tad pievienošana kļūst ļoti vienkārša.
Šādā gadījumā mums vienkārši jāpievieno skaitītāji, un saucējs paliks nemainīgs.
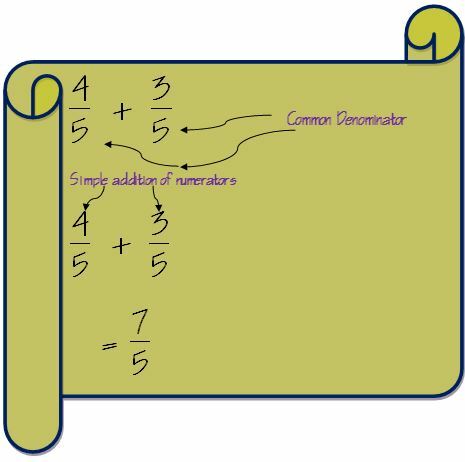
Bet, ja saucēji nav vienādi, mums abu frakciju saucēji jāpadara vienādi. Metode, kas jādara, ir atrast vismazāko kopsaucēju no saucējiem.
Kā atrast vismazāk izplatīto vairākkārtēju
Pieņemsim, ka mums jāatrod LCM ar diviem skaitļiem 8 un 12.
Vispirms atsevišķi pierakstiet abu skaitļu galvenos faktorus.
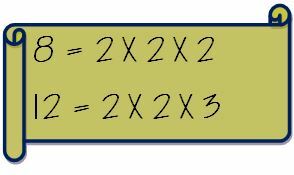
Tagad izņemiet kopējos faktorus un reiziniet tos ar ne bieži sastopamajiem faktoriem. Tātad LK 8 un 12 tiks aprēķināti šādi.
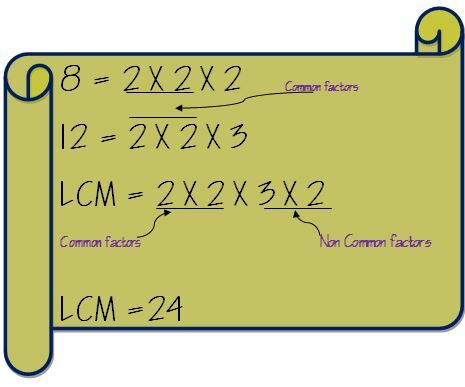
Pievienojiet frakcijas ar dažādiem saucējiem
Pieņemsim, ka mums ir divas frakcijas 3/8 un 5/12
Darbības ir šādas:
1. Pārbaudiet, vai abās daļās saucēji ir vienādi. Ja saucēji ir vienādi, mēs izmantojam iepriekš minēto metodi. Mūsu gadījumā tie ir atšķirīgi.
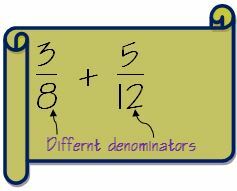
2. Uzziniet saucēja LCM. Kā parādīts iepriekš, LCM 8. un 12. skaitlim ir 24.
3. Abus saucējus padariet tādus pašus kā LCM, reizinot ar piemērotiem skaitļiem.
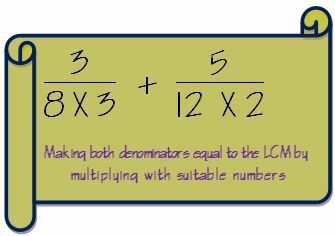
4. Ja mēs reizinājām saucēju ar skaitli, mums arī reizināt skaitītāju ar to pašu skaitli, lai frakcija paliktu neskarta.

5. Veicot šīs darbības, mēs iegūstam divas daļas, kuru saucēji ir vienādi. Tāpēc mums vienkārši jāpievieno skaitītāji, kā mēs to darījām iepriekšējā piemērā.

6. Mēs iegūstam rezultātu kā 19/24
7. Pēc pievienošanas ir jāpārbauda, vai starp skaitītāju un saucēju ir vai nav kopēju faktoru.
8. Ja nav kopēja faktora, rezultātu varam paziņot kā galīgo atbildi.

2. metode
Šī metode arī dos mums vēlamo rezultātu, taču tā nav ieteicama piektās klases skolēniem, kuri vēlas iemācīties pievienot frakcijas.
1. Konvertējiet abas daļas skaitļos, dalot skaitītāju ar saucēju

2. Tagad tas ir vienkārši divu skaitļu pievienošana
3. Pievienojiet divus skaitļus, lai saņemtu atbildi

Lūdzu, ņemiet vērā, ka atbildes, kuras mēs saņēmām 1. un 2. metodē, lai pievienotu frakcijas, ir vienādas. Atbilde pēc 1. metodes ir 19/24. Ja mēs dalīsim 19 ar 24, mēs saņemsim atbildi kā 0,791, ko mēs saņēmām ar 2. metodi.