Schlagen Sie eine einfachere Methode zum Addieren von Brüchen vor

Nun, Brüche können wirklich beängstigend sein, das muss ich zugeben. Brüche zu addieren ist noch beängstigender. Es scheint, als wären sie der Ausgangspunkt für die Schrecken der Welt der Mathematik. Bis Sie erkennen, dass der Umgang mit Brüchen auch so einfach ist wie der Umgang mit natürlichen Zahlen, wenn Sie den Trick kennen.

Methoden zum Hinzufügen von Brüchen

Methode 1

1. Lassen Sie uns zuerst die Terminologie von Brüchen verstehen, bevor wir zu Schritten zum Addieren von Brüchen übergehen. Ein Bruch besteht aus zwei Teilen – Zähler und Nenner. Wenn Sie wirklich ein Gelehrter in Fractions werden möchten, besuchen Sie die Fraktionsseite auf Wikipedia.

Zähler ist die Zahl oberhalb der Linie in einem Bruch und Nenner ist die Zahl unterhalb der Linie.

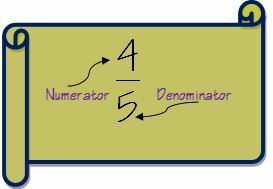
Der erste Schritt zum Addieren von Brüchen besteht darin, die Nenner der beiden Brüche zu überprüfen. Wenn der Nenner für beide Brüche gleich ist, wird die Addition sehr einfach.

In einem solchen Fall müssen wir nur die Zähler addieren und der Nenner bleibt gleich.

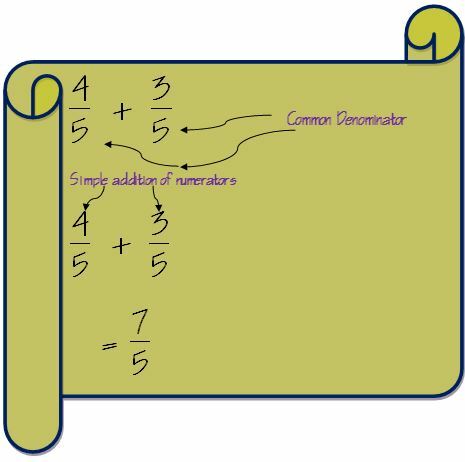
Aber wenn die Nenner nicht gleich sind, müssen wir die Nenner beider Brüche gleich machen. Die Methode besteht darin, das kleinste gemeinsame Vielfache der Nenner zu finden.

So finden Sie das kleinste gemeinsame Vielfache

Angenommen, wir müssen LCM von zwei Zahlen 8 und 12 finden.

Schreiben Sie zunächst die Primfaktoren der beiden Zahlen getrennt auf.

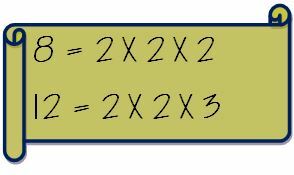
Nehmen Sie nun die gemeinsamen Faktoren heraus und multiplizieren Sie sie mit den nicht-gemeinsamen Faktoren. Der LCM von 8 und 12 wird also wie folgt berechnet.

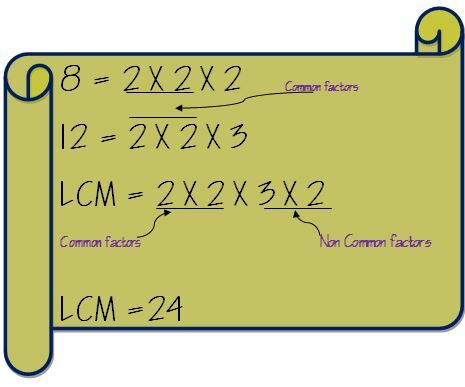
Brüche mit verschiedenen Nennern addieren

Sagen wir, wir haben zwei Brüche 3/8 und 5/12

Die Schritte sind:

1. Überprüfe, ob die Nenner beider Brüche gleich sind. Wenn die Nenner gleich sind, folgen wir der oben genannten Methode. In unserem Fall sind sie anders.

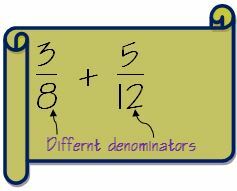
2. Finden Sie den LCM des Nenners heraus. Wie oben dargestellt, beträgt die LCM für 8 und 12 24.

3. Machen Sie beide Nenner gleich dem LCM, indem Sie mit geeigneten Zahlen multiplizieren.

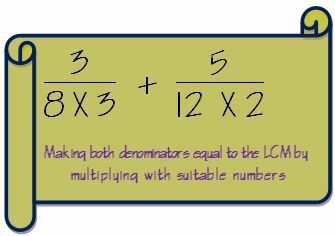
4. Wenn wir den Nenner mit einer Zahl multipliziert haben, müssen wir auch den Zähler mit derselben Zahl multiplizieren, um den Bruch intakt zu halten.

5. Durch Ausführen dieser Schritte erhalten wir zwei Brüche, deren Nenner gleich sind. Wir müssen also nur die Zähler hinzufügen, wie wir es in unserem vorherigen Beispiel getan haben.

6. Wir erhalten das Ergebnis als 19/24

7. Wir müssen prüfen, ob es einen gemeinsamen Faktor zwischen Zähler und Nenner gibt oder nicht, nachdem die Addition durchgeführt wurde.

8. Wenn es keinen gemeinsamen Faktor gibt, können wir das Ergebnis als unsere endgültige Antwort angeben.

 Methode 2

Diese Methode wird uns auch das gewünschte Ergebnis liefern, ist jedoch nicht für Schüler der fünften Klasse geeignet, die lernen möchten, Brüche zu addieren.

1. Wandeln Sie beide Brüche in Zahlen um, indem Sie Zähler durch Nenner dividieren

2. Jetzt ist es eine einfache Addition von zwei Zahlen

3. Addiere die beiden Zahlen, um die Antwort zu erhalten

Bitte beachten Sie, dass die Antworten, die wir in Methode 1 und Methode 2 zum Addieren von Brüchen erhalten haben, gleich sind. Die Antwort von Methode 1 ist 19/24. Wenn wir 19 durch 24 teilen, erhalten wir die Antwort 0,791, was wir mit Methode 2 erhalten haben.